Relação de Euler

A relação criada pelo matemático suíço Leonhard Euler possui extrema importância na determinação do número de arestas, vértices e faces de qualquer poliedro convexo e alguns não convexos. Essa relação permite que os cálculos sejam realizados no intuito de determinarmos o número de elementos de um poliedro. A fórmula criada por Euler é a seguinte:

V – A + F = 2, onde V = número de vértices, A = número de arestas e F = número de faces.


Exemplo 1

Determine o número de faces de um sólido que possui 10 arestas e 6 vértices.
Resolução:
V – A + F = 2
6 – 10 + F = 2
–4 + F = 2
F = 4 + 2
F = 6
Portanto, o sólido possui 6 faces.

Exemplo 2

Determine o número de vértices da pirâmide quadrangular a seguir:

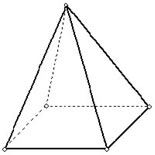
Visivelmente podemos afirmar que a pirâmide possui 5 vértices, 5 faces e 8 arestas. Vamos agora demonstrar que a relação de Euler é válida na determinação dos elementos da pirâmide de base quadrangular.
Resolução:
Vértices
V – A + F = 2
V – 8 + 5 = 2
V = 2 + 3
V = 5

Arestas
V – A + F = 2
5 – A + 5 = 2
–A = 2 – 10
–A = –8 x(–1)
A = 8

Faces
V – A + F = 2
5 – 8 + F = 2
–3 + F = 2
F = 2 + 3
F = 5

Podemos notar que a relação de Euler é realmente válida na determinação dos elementos de um sólido convexo.

Exemplo 3

O número de faces de um poliedro convexo de 22 arestas é igual ao número de vértices. Determine, utilizando a relação de Euler, o número de faces do poliedro.
Resolução:
Considerando que o número de faces é igual ao número de vértices, podemos representar os valores desconhecidos pela incógnita x. Dessa forma, F = x e V = x.

Aplicando a relação de Euler:
V – A + F = 2
x – 22 + x = 2
2x = 2 + 22
2x = 24
x = 12

Portanto, o número de faces do poliedro com 22 arestas é igual a12.